– Alam, M.-R., Liu, W and Haller, G. “Closed Loop Separation Control: An Analytic Approach”, Physics of Fluids, 18 (4): Art. No. 043601 APR 2006. (PDF)
- Wave Carpet
- Bragg Resonance
- Localization
- Wave Resonance
- Ocean Wave Energy
- Separation in Unsteady Flows
- Wave-Mud Interaction
- Caravan in Rough Canal
- Acoustics of Sound-holes
- Mobile Path Planning
Wave Carpet: An Efficient and Multidirectional Ocean Wave Energy Converter

Project in the News
Synopsis
Did you know that we can use the power of ocean waves to generate electricity and fresh water? At UC Berkeley we are developing a new Wave Energy Converter that is able to efficiently harvest this energy. The design was inspired by the ability of muddy seafloors to effectively absorb overpassing ocean wave within only a couple of wavelengths. Our design uses a synthetic-seabed-carpet that is connected to a grid of generators underneath, that has the ability to extract wave energy the same way the muddy seafloor does. We successfully demonstrated its capability to absorb and convert wave energy for multiple sea states. The ability to cancel waves can be used to create safe zones in the ocean, prevent erosion and protect harbors. Secondly, the CWEC’s primary energy conversion creates seawater at high pressure. This can be used to generate electricity, be used for desalination and for the distribution of fresh water. High pressure water can supply pumped-storage hydroelectric power plants, which are the most efficient way to balance the electrical grid.
Why Ocean Wave Energy?
World-wide demand for electricity is expected to double within the next 20 years and thus, one of the major engineering challenges of the 21st century is to meet the constantly increasing global energy demand, especially on the coastlines, as migration is likely double the population in this area by 2025. The ocean is a large, relatively untapped renewable energy resource. The British Department of Trade and Industry has claimed that there are at least 90 million gigawatts of energy in wind driven waves alone worldwide. This may be compared to the 15 thousands gigawatts of energy consumed worldwide. According to London-based Carbon Trust, wave energy can realistically provide over 2,000 terawatt hours (TWh) of electricity per year approximately 10% of global electricity needs and eventually generate revenues from wholesale power sales in excess of $50 billion per year. However, according to the Electric Power Research Institute (EPRI) of Palo Alto, CA, a realistic estimate of ocean wave energy potential in the United States indicates approximately 6% of total energy needs with a wholesale market value eventually reaching $16 billion per year.
Although still in the early stages of development, wave energy can and will provide enough power to supply a substantial part of the world energy demand. The wave energy industry is sometimes compared with the wind energy industry some 25 years ago when there was neither a unique design, nor a universal agreement on its future path. Wind industry has converged to a unique design over the past quarter of a century and now is a major player in the energy industry. Having learned from the evolution of wind power, wave energy is expected to come into play in a much shorter time period.
Wave Carpet: Inspired by Nature
The ability of muddy seafloors to dampen ocean waves is well documented at various locations around the world. In the Gulf of Mexico, fishermen have learned to steer their boats into a local muddy spot known as the “mud hole” when a storm is brewing. Here, the wave–mud interaction is so strong that the storm waves are damped within a distance of a couple of wavelengths (100–200 m) and the boats there are completely safe.
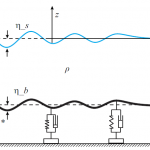
If mud can seriously take so much energy out of ocean waves, then why don’t we use this idea to design a wave-energy converter that’s very efficient? We came up with the idea of using a viscoelastic carpet of wave-energy conversion (CWEC) placed over a network of vertically oriented springs and generators on the coastal seafloor. The flexible carpet responds just like mud: as waves pass overhead, they induce dynamic ripples and undulations in its sprung surface, and these perturbations can be used to generate electricity.
Wave Carpet: How It Works
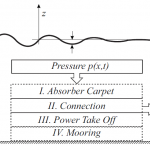
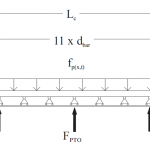
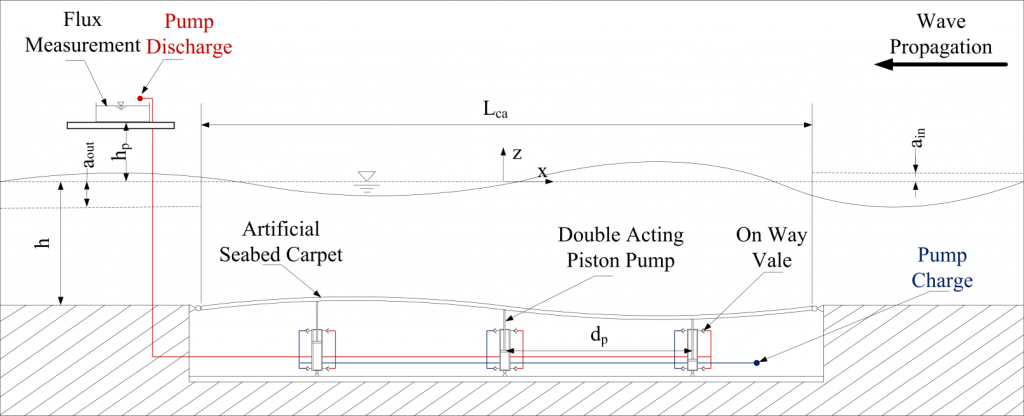
The principle components of the prototype consist of a synthetic seabed carpet, a direct physical connection, a hydraulic Power Take Off system and a mooring system.
1) Schematic of a synthetic viscoelastic carpet on the seafloor for extracting energy from surface gravity waves. 2) Abstract model of components. 3) Mechanical model.
Here at UC Berkeley, we are working on a novel design to harvest Wave Energy economically and reliably. In our wave tank laboratory, we have developed a proof-of-concept-prototype and have successfully tested the functionality and ability of the converter to cancel waves and generate power. The concept has been investigated theoretically and numerically for linear and nonlinear regimes. It has undergone extensive experimental study at our wave tank laboratory.
The energy stored in overtopping waves is damped out by the absorber carpet and converted into hydraulic energy using double reacting reciprocating pumps which are connected to the carpet. The engineering challenge of an absorber carpet material with anisotropic material properties was addressed by using a composite material. The carpet material required a low Young’s modulus in its horizontal direction and a high bending stiffness in its vertical direction. The results of the experiments conducted are first data sets for the absorption and Power Take Off (PTO) efficiency while operating under the influence of several sea states.
This New Design has distinct advantages:
- High survivability – Due to the fact that the carpet is seabed-based, it is able to survive the strong momentum of stormy seas.
- Material Durability – Flexible non-corrosive material.
- Transportability – The system is easily moved and brought to the ocean without requiring high maintenance costs.
- Efficiency – Ability of high, broadband and omnidirectional absorption efficiency.
- Scalability – The modular design allows the device to scale in width for setting a desired output power capacity.
- Hazardless – The device poses no visual pollution to the ocean surface and no collision danger to boats and sea life.
Our long term goal is to tap the abundant and unused resources of ocean wave power in order to contribute to the RE mix and thereby meet the future’s growing energy demand in an independent and sustainable manner.
An essential step towards this goal is to fully proof the functionality of a pilot plant in the ocean.
Publications
- Lehmann, M., Elandt, R., Pham, H., Ghorbani, R., Shakeri, M., and Alam, M.-R., “An artificial seabed carpet for multidirectional and broadband wave energy extraction: Theory and Experiment”, Proceedings of 10th European Wave and Tidal Energy Conference, EWTEC2013, 2-5 Sept. 2013, Aalborg, Denmark.[PDF]
- Alam, M.R., “A Flexible Seafloor Carpet for High-Performance Wave Energy Extraction”, The 31st International Conference on Ocean, Offshore and Arctic Engineering (OMAE 2012), Rio de Janeiro, Brazil, July 1-6, 2012. [PDF]
- Alam, M.R., “Nonlinear analysis of an actuated seafloor-mounted carpet for a high-performance wave energy extraction.”, Proceedings of the Royal Society, A, doi: 10.1098/rspa.2012.0193, June 2012. [PDF]
- Alam, Mohammad-Reza, “Wave Energy”, IRIS Magazine, Technology Avenue, Issue 1, Summer 2008, Pages 12-13. [PDF]
Bragg Resonance with Regular Topography
Bragg Resonance in a 2-Layer Fluid
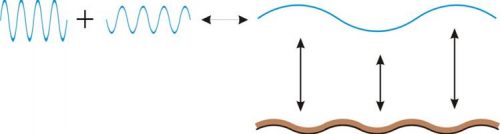
Real ocean density is not constant and varies with the depth (due to change in water temperature and salinity). In most oceans, density jumps from a lighter upper layer fluid density to a heavier lower layer fluid one over a surface called Thermocline. Waves – similar to surface waves – can propagate over Thermocline and are called internal (interfacial) waves. Internal waves, when they propagate over topography, may exchange energy (via nonlinear resonance) with surface waves. If bottom is periodically modulated, the phenomenon is called Bragg Resonance and very well understood for a homogeneous fluid. Bragg resonance of internal waves is important in explaining the generation of internal gravity waves particularly in littoral zones, dead water phenomenon (high resistance on ships in stratified waters), and has many applications in navigation and design of off-shore structures.
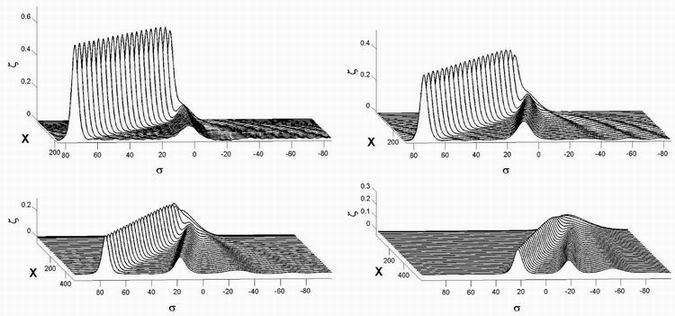
We have studied Bragg resonance of interfacial waves theoretically and numerically. Starting from perturbation analysis, and proceeding to higher order nonlinearities, closed-form solutions for the resonance condition and the growth rate of resonant waves are obtained. Part II of this work is devoted to the development of a very efficient spectral-based numerical scheme. Theoretical results are cross-validated with our direct simulation and effect of higher nonlinearity and complicated cases – which are beyond the capacity of analytical tools – are studied. It is shown for example, that by multiple resonances between a chosen set of waves, water surface may undergo chaotic oscillations. We also show that Bragg resonance in two-layer fluids can significantly contribute to the development of the ocean spectrum, and, is a potential mechanism for the mysterious phenomenon of generation of high-frequency interfacial waves in lakes and on continental shelves.
References:
– Alam, M.R., Liu, Y. and Yue, D.K.P., “Bragg resonance of waves in a two-layer fluid propagating over bottom ripples. Part I. Perturbation analysis.”, J. Fluid Mechanics, Volume 624 (2009), pages 191-224. [PDF]
– Alam, M.R., Liu, Y. and Yue, D.K.P., “Bragg resonance of waves in a two-layer fluid propagating over bottom ripples. Part II. Numerical simulation.”, J. Fluid Mechanics, Volume 624 (2009), pages 225-253. [PDF]
– Alam, M.R., Liu, Y. and Yue, D.K.P., “Chaotic Internal Wave Motion due to Multiple Bragg Resonances”, American Geophysical Union Fall Meeting. San Francisco, CA, 15-19 December 2008.
Localization over a Random Bottom
Localization of Internal Waves by Random Topography
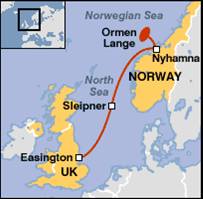
If waves travel over a random bathymetry, strong spatial attenuation occurs due to multiple scattering (c.f. Anderson localization in solid-state physics). Unlike Bragg scattering where strong resonance occurs for a discrete set of frequencies satisfying the Bragg resonance condition, spatial attenuation takes place at nearly all wave frequencies in disordered media. Our consideration of localization in stratified waters was motivated by the need of Ormen-Lange gas extraction project in North Sea to estimate the impact of long-period internal waves on gas pipelines. Evolution of internal solitary waves and the effect of harmonic-generation in time-periodic waves traveling over random topography were studied.
References:
– Alam, M.-R. and Mei, C.C., “Ships advancing near the critical speed in a shallow channel with a randomly uneven bed”, J. Fluid Mechanics, Volume 616 (2008), pages 397-417. [PDF]
Ship wave resonance in stratified seas
Waves of an unsteady disturbance in a 2-layer fluid

Oscillation of underwater vehicles (particularly submarines) in littoral zones, where water is more likely to be stratified, generates particular waves that can reveal information about size, speed and the depth of the vehicle. We studied the mechanism behind the generation of these waves and their interactions. For a steadily translating and sinusoidally oscillating disturbance in a two-layer fluid, up to eight waves may appear on the water surface/interface. Unlike in homogeneous fluid, nonlinear resonance can occur between these eight waves. We theoretically found, and numerically validated, that existence of stratification along with second-order nonlinearities can result in generation of a series of new waves that can travel away or toward the disturbance.
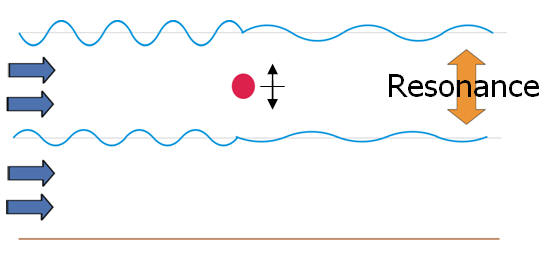
Artist rendering of disturbance wave resonance in a 2-layer density stratified fluid:
Assume our pirate is driving his (or her?) submarine in a strong stratified ocean well below the water surface. If the captain pirate does not know any math, he thinks that he is fully concealed from the police boats on the surface. But fortunately (or unfortunately!) at a specific speed situation changes. At that speed, it will send a signal (of course due to nonlinearity) to the surface…. you watch the fate of the poor captain pirate !!!
References:
– Alam, M.R., Liu, Y. and Yue, D.K.P., “Waves due to an oscillating and translating disturbance in a two-layer density stratified fluid”,J. Engineering Mathematics, Volume 65 (2009), Issue 2 Pages 179–201. [PDF]
– Alam, M.R., Liu, Y. and Yue, D.K.P., “Resonance Interaction of Ship waves in Stratified Seas”, Submitted to J. Fluid Mechanics.
Ocean wave energy

World-wide demand for electricity is expected to double within the next 20 years; this, combined with commitments to significantly reduce CO2 emissions in the same time-frame are increasing the search for clean, socially acceptable methods of generating power. Ocean waves are a large, relatively untapped renewable energy resource. According to London-based Carbon Trust, wave energy can realistically provide over 2,000 TWh/year of electricity–approximately 10% of global energy needs. Ocean waves and tidal currents are one of the most important, clean, cheap, rich, and reliable sources of renewable energy on the earth. Ocean energy in Europe has attracted a good deal of attention since 1970’s (about 30 companies and research institutes). The instability in the oil price, environmental issues, and finiteness of resources has made the Unites States to seriously investigate on ocean wave energy companies. It is sought to be a very potential and active area of research in the next decades. Although still in the early stages of development, ocean energy can and will provide enough power to supply a substantial part of the world energy demand. The wave energy industry is sometimes compared with the wind energy industry some 25 years ago when there was neither a unique design, nor a universal agreement on its future path. Wind industry has converged to a unique design over the past quarter of a century and now is a major player in the energy industry. Having learned from the evolution of wind power, wave energy is expected to come into play in a much shorter time period.
Demonstration of an experimental study on “free floating point absorber wave energy converter (WEC)” performed at MIT Parsons Lab on October 2008. (James Sannino and M.-R. Alam)
Full scale prototype of our free floating wave energy converter to be deployed in the Gulf of Maine. Newbury port, Massachusetts, January 2009.
Artist rendering of Resolute Marine Energy’s Millipede (Bonus question: why do we have/want bouncing in the right movie?)
References:
– Alam, Mohammad-Reza, “Wave Energy”, IRIS Magazine, Technology Avenue, Issue 1, Summer 2008, Pages 12-13.(PDF)
– Alam, M.R., Sannino, J., Goudy, G., Monteith, I., Page, S., Staby, B., “ Investigation on the performance of a free-floating point-absorber wave energy converter deployed in the Gulf ofMain”, Preprint.
– Sannino, J. and Alam, M.R. “Energy Extraction from Ocean Waves: A Direct Approach” The 2008 MIT Energy Conference: Energy Exhibition and Showcase, April 11th 2008, Cambridge Marriot Hotel, Cambridge, Massachusetts.
Feedback Control of Separation in Unsteady Flows
Separation of flow is responsible for most of the form drag on airplanes, stall in turbine blades and vortex shedding and vortex induced vibration of objects placed in fluid flow. Controlled separation, however, has practical applications and is used, for example, to enhance the mixing efficiency in combustion chambers. Although criteria for steady separation were known since Prandtl’s article (1904), it took a century long for the unsteady counterpart to be discovered. George Haller (JFM 2004) gave dynamical-systems based rigorous criteria for flow separation in unsteady flows.
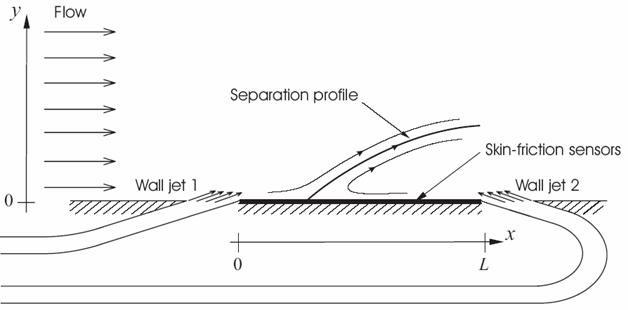
We developed, for the first time, a general (Reynolds independent) analytical closed-loop algorithm for controlling the location of unsteady separation and reattachment in two-dimensional Navier-Stokes flows. Our controller enforces the Haller’s exact kinematic separation criteria and hence creates wall-based unstable manifolds at prescribed locations. The underlying control algorithm is based on the exact wall-shear evolution equation, a one-dimensional nonlinear partial differential equation (PDE) defined on the wall between two discrete actuators. Performance of the controller is studied numerically by implementation over a full Navier-Stokes fluid.
Numerical simulation of effectiveness of our analytical feedback control for controlling the point of separation in an unsteady flow. Red lines show instantaneous streamlines (note that instantaneous separation point denoted by the red triangle is a moving all the time). The blue curves are streaklines (i.e. I am injecting dye particles at four points on the wall). Black triangle points out the desired separation point. Eventually the streaklines will point out the right separation point and show that our controller indeed works.
References:
Wave-Mud Interaction
Damping of the ocean surface waves as they propagate over and interact with the muddy seafloor plays an important role in coastal phenomena. Fishermen of southwest coast ofIndia in ”Chakara” feast celebrate the arrival of mud banks that damp large monsoon-driven waves and calm onshore waters resulting in a rich fish harvest.
Due to the strong effect of the seafloor on the wave characteristics, particularly in very muddy regions like gulf of Mexico, the underlying mechanism and ability of prediction of coastal wave condition is of central interest. There are a number of models used to describe the mud in the wave attenuation problem. In general, these models are constitution relations for the mud. The mud nature, however, is very complicated and among these several models already existing none of them are capable of generally describing the damping phenomenon. we came up with a visco-elastic three-parameter bottom model in which all complexities are in the coefficients (rather than the equations). We also developed a higher order spectral method based algorithm from which phase-resolved simulation of ocean waves can be performed (in a phase resolved simulation we model the ocean surface as is seen in real nature, as opposed to phase averaged model that only studies some long term averaged quantities of the ocean, such as the spectrum). The phase -resolved tool along with our visco-elastic model has made a strong tool for the study of the linear damping and nonlinear interaction of waves over muddy shallow water. Comparison of our direct simulation results with field observations and previous theories shows the effectiveness of our approach. We include the effect of nonlinearity, shoaling and frequency dependent mud damping together in a realistic ocean situation.

References:
– Alam, M.R., Liu, Y. and Yue, D.K.P., “Numerical Investigation of Broadband Wave Attenuation over Muddy Shoaling Seabeds”, Submitted to the Geophysical Research Letter (2009).
– Alam, M.R., Liu, Y. and Yue, D.K.P., “Numerical Investigation of Dissipation Mechanisms for Surface Wave Propagation over Muddy Seabed”, AGU Chapman Conference on Physics of Wave-Mud Interaction, Amelia Island, Florida, USA, 17-20 November 2008.
– Alam, M.R., Liu, Y. and Yue, D.K.P., “Broadband Waves over Muddy Seafloors” March meeting of American Geophysical Union: 2008 Ocean Sciences Meeting, From the Watershed to the Global Ocean, 2-7 March 2008 Orlando-Florida.
A caravan of fast ships in a wide rough canal
It is known that when a boat advances near critical speed in a wide canal, solitons can be radiated upstream in a transient manner. Real canals are not flat, therefore we considered a canal with a randomly rough bed. Governing equations were shown to be in the form of forced-damped KdV equation and numerical evaluations showed less transient behavior in forces and moments. However, striking results emerged when we considered an array of ships advancing in the canal. When a caravan of ships moves over a flat (with no bathymetry undulation) canal, bow and stern waves unsteadily interact resulting in irregular and extreme forces and moments from time to time. But surprisingly, if roughness is taken into account and in a relatively short transient time, the bow wave of a front ship upon encountering and interacting with the stern wave of a back ship forms a smooth steady pattern: another miracle of nonlinear equations.
If you are wondering where on the planet we may get an array of ships moving in a canal, here are a couple of examples: The left photo depicts early steam ships in the Suez canal (about 1880) and the right photo is a picture supplied by Stella Elliott (BBC) USS AMERICA (CV 66) during its transit through the Suez canal.
Right: Ship caravan over a flat bottom, Left: Ship Caravan over a randomly rough bottom (for more information see the references)
References:
– Alam, M.-R., Liu, W and Haller, G. “Closed Loop Separation Control: An Analytic Approach”, Physics of Fluids, 18 (4): Art. No. 043601 APR 2006. (PDF)
Acoustics of Sound-holes in Musical Instruments
The present day violin is acoustically so sophisticated that 200 years of scientific study has not been able to systematically distinguish between a good and an average violin. The present-day violin making is based on replicating old Italian violins widely accepted as perfect instruments; a perfection that is reached only by hands of artist, and not yet reproducible by quantitative scientific methods. One of the major questions is the driving forces in the evolution of f-hole’s geometrical design that has ended up to the present-day f-shape. The main contribution of f-hole in violin is to amplify the sound radiation (air resonance) at low frequencies, at which the soundboard is inefficient in sound radiation.
The efficiency of sound radiation at low frequencies in musical instruments is improved by the use of a sound hole. The sound hole enhances the radiation of sound by vibrating the volume of air inside as well as near its opening. A common example is an empty bottle: the air inside vibrates when you blow across the top, and enhances the radiated sound. This phenomenon, called the Helmholtz resonance, is utilized in musical instruments to enhance the radiation of sound at low frequencies.
An important characteristic of the sound-hole is the frequency at which the radiated sound is enhanced the most. This frequency, called the resonance frequency, can easily be obtained for holes with simple geometries such as the circular hole in guitar (see The Theory of Sound, vol. 2 by Lord Rayleigh). For the sound holes with complicated shapes such as f-holes or lute rosettes (See below), finding the resonance characteristics is much more challenging.
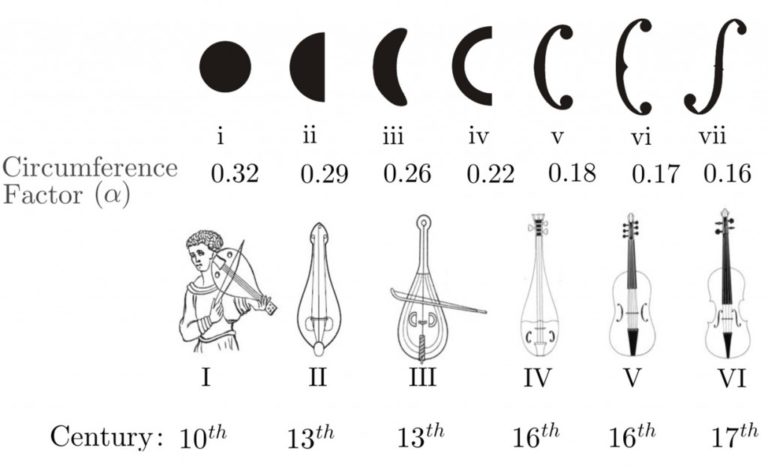
Utilizing experimental and numerical simulation techniques, we showed that the evolution of violin moves toward acoustic power efficiency: for a constant void area, f-hole has the maximum power radiation among other historic soundhole geometries in the violin family: circular opening (10th-century viols), semi-circular opening (Lyras in 13th century), crescent and semi-circular strip (13th century), primary c-hole and c-hole (early viols and violins in 16th century), and present-day f-hole in violins (unchanged since 17th century).
The historic developmental path from circular soundhole to the present-day f-hole goes toward maximizing radiation at air resonance for a fixed void area. Comparing an f-hole to a circular soundhole with the same void area, the resonance frequency, f, of the f-hole differs from the one of the circular by 4 semitones. Treating the radiation of sound during resonance as a monopole, the radiating power W has a power law relationship with the resonance frequency as , which results in 4.5 dB higher radiating power in f-hole compared to circular opening with the same area. Our method of analysis was verified by measuring the resonance and bandwidth of different openings on a standard resonance box (see Fig below)
Thanks to Johnson String Instrument we had the chance to verify our results experimentally on a number of very good instruments:
References:
– Tavakoli Nia, H., Alam, M.-R., Liu, Y., and Makris, N., “Acoustics efficiency of Soundholes in Musical Instrument”. To be submitted.
More Photos:
Optimally Stable Mobile Manipulator Path Planning
Mobile manipulators such as mechanical loaders and rescue robots consist of a moving base and a one (or multi) degree of freedom arm attached to the base. In many circumstances mobile manipulators are supposed to move on uneven terrains and may get into postures dangerous for their stability. The aim of my work was to develop and implement an active real-time feedback control to be installed on such vehicles to enhance their stability by static and dynamic compensatory motion of their arms. This compensatory motion is similar to what our hands do when we are about to fall down.
Examples of Mobile Manipulators in real life
Classical control methods are based on closed form or approximate analytical solutions which – although very good in simple less degree of freedom robots- in real many degree of freedom mobile manipulators are very slow and non-reliable. For high degree of freedom robots, inherent complexity of equations and the need to real-time answers to the optimization problem sparked us to apply artificial intelligence techniques. We developed an algorithm that invokes combinatory Artificial Neural Networks and Genetic Algorithms to achieve a robust feedback control. We showed the performance of our approach via many numerical examples.
Schematic of problem definition.
References:
– Meghdari A, Naderi D, Alam M.R., “Neural-network-based observer for real-time tipover estimation”, Mechatronics 15 (8): 989-1004 October 2005. [PDF]
– Meghdari A., Naderi, D. and Alam, M.R., “Tipover Stability Estimation for Autonomous Mobile Manipulator Using Neural Network” Proceedings of the 2004 Japan–USA Symposium on Flexible Automation, JUSFA 2004, pp. 19-25.
– Meghdari A., Naderi, D. and Alam, M.R., “Real-Time Compensatory Manipulator Motion Planning for Stabilizing a Mobile Manipulator” Proceedings of the 2003 ASME Int. Design Engineering Technical Conferences, September 2003, pp. 2-6.
– Alam, M.R., Meghdari A. and Naderi, D., “Optimally Stable Mobile Manipulator Path Planning Using Genetic Algorithm” Proceeding of international conference of mechanical engineering (ISME 2003) Tehran-IRAN.