TAFLab

Theoretical & Applied Fluid Dynamics Laboratory

Feedback Control of Separation in Unsteady Flows

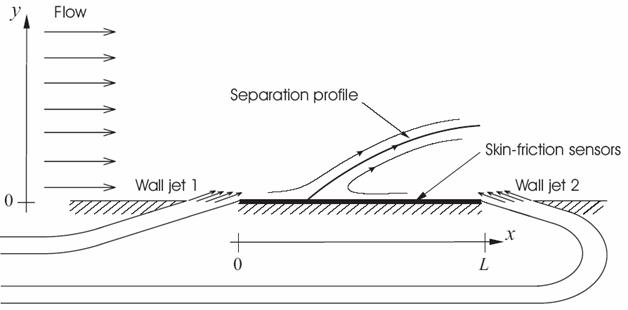
Separation of flow is responsible for most of the form drag on airplanes, stall in turbine blades and vortex shedding and vortex induced vibration of objects placed in fluid flow. Controlled separation, however, has practical applications and is used, for example, to enhance the mixing efficiency in combustion chambers. Although criteria for steady separation were known since Prandtl’s article (1904), it took a century long for the unsteady counterpart to be discovered. George Haller (JFM 2004) gave dynamical-systems based rigorous criteria for flow separation in unsteady flows.

Separation is in charge of most of the drag on flying objects like airplanes and gulf balls

We developed, for the first time, a general (Reynolds independent) analytical closed-loop algorithm for controlling the location of unsteady separation and reattachment in two-dimensional Navier-Stokes flows. Our controller enforces the Haller’s exact kinematic separation criteria and hence creates wall-based unstable manifolds at prescribed locations. The underlying control algorithm is based on the exact wall-shear evolution equation, a one-dimensional nonlinear partial differential equation (PDE) defined on the wall between two discrete actuators. Performance of the controller is studied numerically by implementation over a full Navier-Stokes fluid.

Schematic of the problem configuration. An unsteady flow enters the domain of interest from the left. Two counter propagating wall jets are connected to the controller and have to force a distinct separation at a desired point. The wall (0<x<l) is carpeted with skin friction sensors.

Numerical simulation of effectiveness of our analytical feedback control for controlling the point of separation in an unsteady flow. Red lines show instantaneous streamlines (note that instantaneous separation point denoted by the red triangle is a moving all the time). The blue curves are streaklines (i.e. I am injecting dye particles at four points on the wall). Black triangle points out the desired separation point. Eventually the streaklines will point out the right separation point and show that our controller indeed works.

References:

– Alam, M.-R., Liu, W and Haller, G. “Closed Loop Separation Control: An Analytic Approach”,  Physics of Fluids, 18 (4): Art. No. 043601 APR 2006. (PDF)